| EZMod Library provide an
innovative and flexible way to describe and manipulate most frequently encountered
optimization problems, to solve them and have access to the solution and other pertinent
results. EZMod Library reduces the
development effort, costs and time for designing and implementing optimization modules in
your applications. Indeed, EZMod Library provides variety of facilities
to develop applications without solver-specific knowledge or expertise.
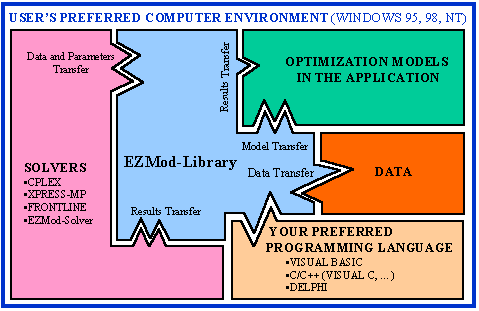
EZMod
Library allows the problem description to be made in the order suggested by the
application logic and not by that of the solver.
EZMod Library takes
care of all the interactions with the solver to be used and establishes the necessary
links between the computer environment, the programming language and the data.
EZMod supports a wide range of commercial solvers
and allow access to their optimization capacity such as CPLEX, XPRESS-MP and FRONTLINE
SYSTEMS without requiring solver-specific knowledge or expertise. EZMod takes care
of all the interactions required by the solver to be used. The interaction between EZMod
and the solver is completely transparent for the developer. The modeling activity is then
independent of the solver to be used. CPLEX, XPRESS-MP and FRONTLINE SYSTEMS solvers are
not equipped to solve Quadratic Mixed Integer Programming (QMIP) problems
but this is no constraint for the EZMod Library users since QMIP
problems are transformed transparently and efficiently to an equivalent MIP problem.
The EZMod-Library functions, their names
and parameters were designed to match the commonly accepted notation in the optimization
community, thus making their use very intuitive. Take a look at the EZMod User Guide with your browser.
EZMod Library is designed for WINDOWS
95/98 and WINDOWS NT and it is accessible from a variety of of modern programming
environment that allows calls to DLLs such as Microsoft Visual Basic, Visual C++,
Borland Delphi, C/C++, C++ Builder.
Generic Format of supported optimization problems
EZMod Library allow to
handle a variety of optimization problems. The generic format of these problems is:
Minimize or Maximize
Z = CX + XtQX
Subject to : AX ~ B
Lw <=
X <= Up |
Where:
| X (n, 1)
Vector |
Decision Variables
which may be continuous, binary or integer |
| C (1, n)
Vector: |
Coefficients of the
objective function linear part |
| Q (n, n)
Matrix |
Coefficients of the
objective function quadratic part |
| A (m, n)
Matrix |
Coefficients of the
constraints matrix |
| B (m, 1)
Vector |
Coefficients of the
constraints right hand side |
| ~ (m,1)
Vector |
Constraints types as
'�', '�' or '=' |
| Lw (1, n)
Vector |
Coefficients of the
variable lower bounds |
| Up (1, n)
Vector |
Coefficients of the
variable upper bounds |
This generic format is:
- Linear Program (LP) if the Q matrix
is null and X contains only continuous variables.
- Quadratic Program (QP)
if the Q matrix is not null and X contains only continuous variables.
- Mixed-Integer Program (MIP) if the Q
matrix is null and X contains at least one integer variable.
- Quadratic Mixed-Integer Program (QMIP) if
the Q matrix is not null and X contains at least one integer variable.
|
